Specifying Orientation Information for Tessellation Cells

Important

Read first: Generating and Meshing a Simple Tessellation and (optionally) Generating and Meshing a Fundamental Region of Orientation Space and Plotting a Pole Figure.

Orientations for the cells can be specified as input, using option -ori. By default, “random orientations” are generated:

$ neper -T -n 1000 -crysym cubic

This generates a Tessellation File (.tess) named n1000-id1.tess.

Note

  • In general, it is important to define the crystal symmetry, using -crysym.

  • It is possible to generate only orientations (no actual tessellation) using -format ori, which only produces an orientation file (technically a Data File) of extension .ori.

  • In the case where an actual tessellation is generated, the cell orientations are generated after (and fully independently of) the tessellation morphology.

The orientations can be visualized on a pole figure using the Visualization Module (-V) and -space pf:

$ neper -V n1000-id1.tess -imagesize 500:500 -space pf -print img1
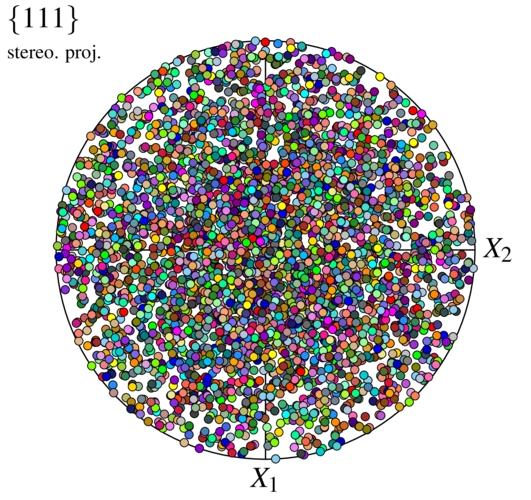
../../_images/img12.png

We recognize a distribution of random orientations. The apparent higher density in the center is due to the use of the stereographic projection (see -pfprojection), and an equal-area projection would effectively produce uniform density.

Using an ODF

An ODF can be specified by providing a mesh of orientation space and intensity values at the mesh elements. A mesh of the fundamental region of Rodrigues space (for the considered crystal symmetry, here cubic) can be generated as follows (see tutorial “Generating and Meshing a Fundamental Region of Orientation Space”):

$ neper -T -n 1 -domain "rodrigues(cubic)" -o fr
$ neper -M fr.tess -cl 0.05

The elemental values of the ODF, which are defined externally, are written in an external file, odf.txt. In the present case, it defines a generic rolling texture of an FCC material. The mesh of orientation space (generated as described above) also is provided by an external file, fr.msh.

Cell orientations can be generated from the ODF as follows:

$ neper -T -n 1000 -ori "odf(mesh=file(fr.msh),val=file(odf.txt))" -crysym cubic

Important

The crystal symmetry must be specified using -crysym and should be the same as the one of the orientation space (fr.msh); otherwise, an error is generated.

The orientations can be visualized as before:

$ neper -V n1000-id1.tess -imagesize 500:500 -space pf -print img2
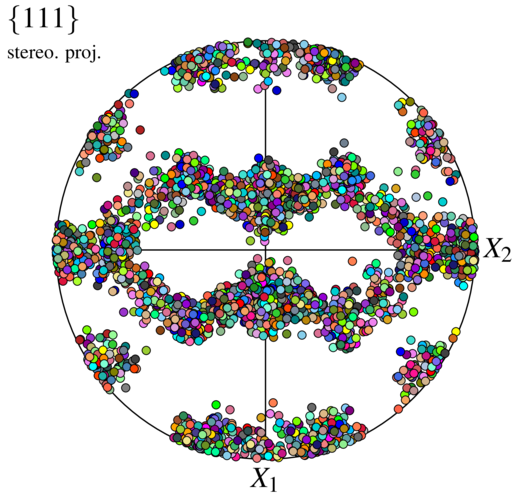
../../_images/img22.png

We recognize a typical rolling texture.

Using Discrete Orientations and Orientation Fibers

An orientation distribution can be defined from “base”, discrete orientations and orientation fibers (see -ori and Rotations and Orientations), optionally surrounded by distributions.

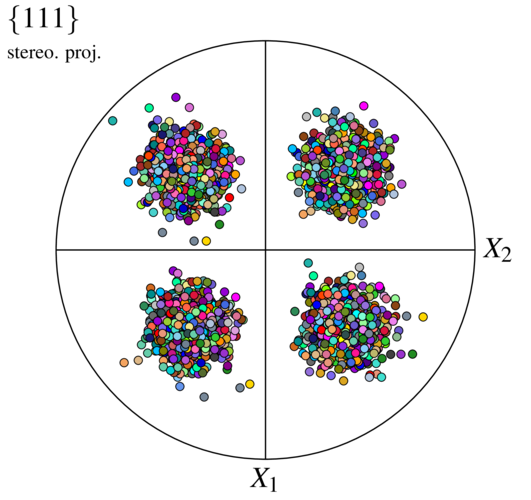
A simple case of a Cube-type orientation distribution can be obtained as follows:

$ neper -T -n 1000 -crysym cubic -ori "Cube:normal(8)"

Note

“normal(8)” generates a distribution about the nominal orientation corresponding to a tri-variate normal distribution (in tangent space, \(r\,\theta\)) of a (1D) standard deviation equal to 8 degrees. When applied to an orientation fiber, the distribution becomes bi-variate (perpendicular to the fiber).

The orientations can be visualized as before:

$ neper -V n1000-id1.tess -imagesize 500:500 -space pf -print img3
../../_images/img32.png

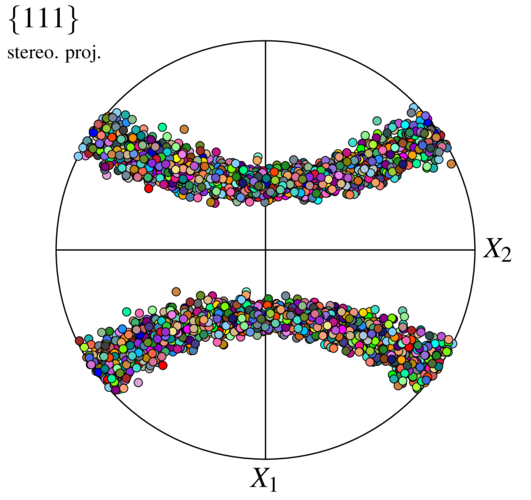
A simple case of a \(\left<1 0 0\right> | X_i\) fiber surrounded by a distribution of a 1D standard deviation of 4 degrees can be obtained as follows:

$ neper -T -n 1000 -crysym cubic -ori "fiber(1,0,0,1,0,0):normal(4)"

The orientations can be visualized as before:

$ neper -V n1000-id1.tess -imagesize 500:500 -space pf -print img5
../../_images/img52.png

Several orientations (or orientation fibers) can be used to produce more complex distributions, each with its own weight and distribution. An example is as follows:

$ neper -T -n 1000 -crysym cubic -ori "2*Brass1:normal(3.9)+2*Brass2:normal(3.9)+S1:normal(4.7)+S2:normal(4.7)+S3:normal(4.7)+S4:normal(4.7)+0.8*Copper1:normal(5.6)+0.8*Copper2:normal(5.6)+Cube:normal(3.9)+2*Goss:normal(3.9)"

The orientations can be visualized as before:

$ neper -V n1000-id1.tess -imagesize 500:500 -space pf -print img4
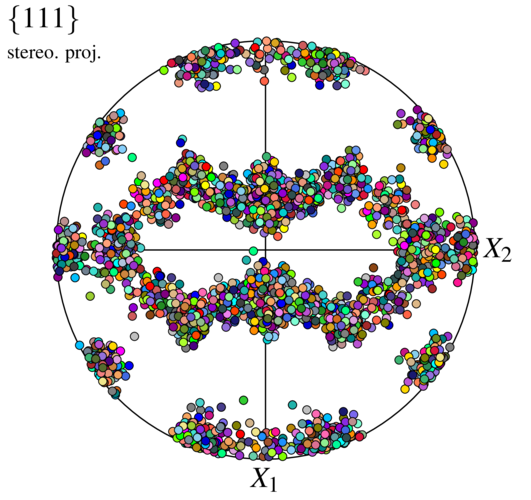
../../_images/img42.png

Incidentally, it is similar to the one generated in Using an ODF.