Generating and Meshing a Fundamental Region of Orientation Space
Important
Read first: Generating and Meshing a Simple Tessellation.
Fundamental regions of Rodrigues orientation space can be generated as tessellation domains, using -domain, for any crystal symmetry (cubic, hexagonal, etc.).
Once defined as a domain, a fundamental region can be tessellated and meshed just as any other domain.
A mesh of the fundamental region is necessary, for example, in the Simulation Module (-S), to define the orientation space (-orispace).
Due to the particularity of the fundamental region of orientation space, it is also possible to enforce periodicity relationships between equivalent faces, i.e. faces that represent equivalent orientations, even if the domain does not have a periodic shape (the same goes for equivalent edges and vertices).
Generating and Meshing a Standard Fundamental Region
A fundamental region can simply be generated using -domain, by specifying the crystal symmetry. For example, for cubic and hexagonal crystal symmetries:
$ neper -T -n 1 -domain "rodrigues(cubic)" -o fr-cub
$ neper -T -n 1 -domain "rodrigues(hexagonal)" -o fr-hex
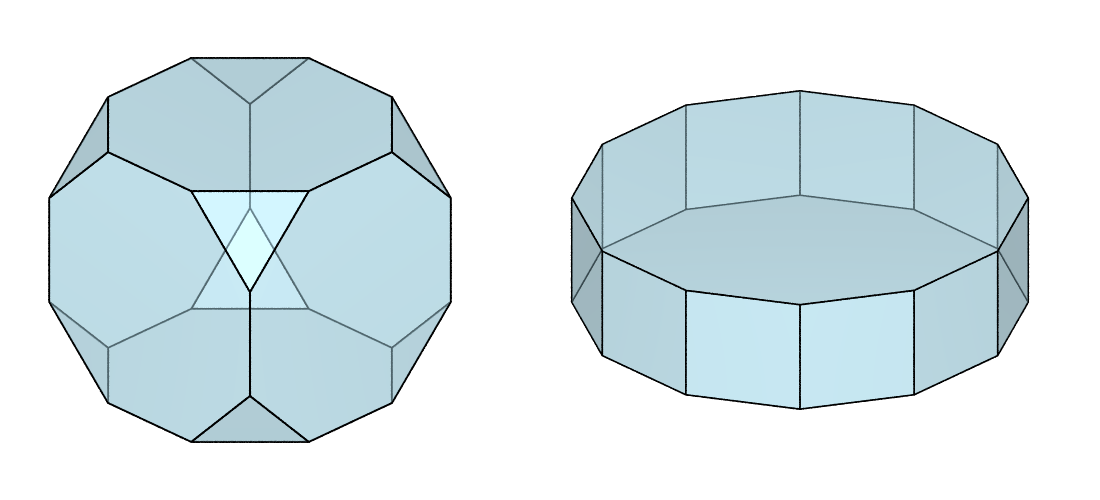
A fundamental region is best visualized in nearly-isometric, orthographic projection. We can also adjust the cell and edge properties for better rendering:
$ neper -V fr-cub.tess -datacellcol lightblue -datacelltrs 0.5 -dataedgerad 0.003 -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 500:500 -cameraangle 13 -print fr-cub
$ neper -V fr-hex.tess -datacellcol lightblue -datacelltrs 0.5 -dataedgerad 0.004 -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 600:500 -cameraangle 24 -print fr-hex
$ convert +append fr-cub.png fr-hex.png fr1.png
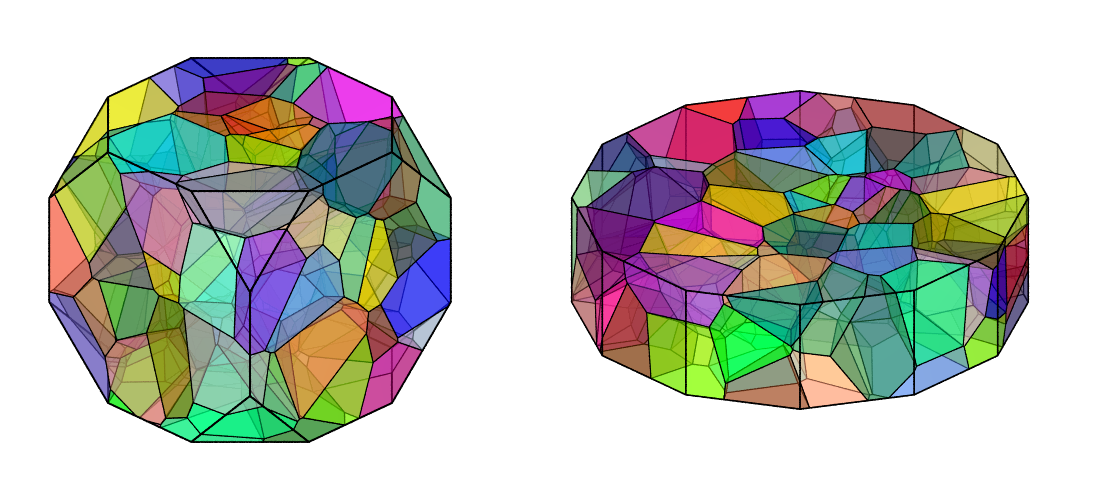
An internal tessellation can be generated as for any other domain. For example, to generate a simple 100-cell tessellation:
$ neper -T -n 100 -domain "rodrigues(cubic)" -o fr-cub100
$ neper -T -n 100 -domain "rodrigues(hexagonal)" -o fr-hex100
Again, we adjust the cell and edge properties for better rendering:
$ neper -V fr-cub100.tess -datacelltrs 0.5 -dataedgerad "((domtype==1)?0.003:0.002)" -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 500:500 -cameraangle 13 -print fr-cub100
$ neper -V fr-hex100.tess -datacelltrs 0.5 -dataedgerad "((domtype==1)?0.004:0.003)" -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 600:500 -cameraangle 24 -print fr-hex100
$ convert +append fr-cub100.png fr-hex100.png fr3.png
The generated tessellations (either 1-cell or 100-cell) can be meshed. For example, with 1 cell (untessellated fundamental regions):
$ neper -M fr-cub.tess -cl 0.1
$ neper -M fr-hex.tess -cl 0.1
$ neper -V fr-cub.tess,fr-cub.msh -dataelsetcol lightblue -showelt1d all -dataelt1drad 0.003 -dataelt3dedgerad 0.0015 -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 500:500 -cameraangle 13 -print fr-cub
$ neper -V fr-hex.tess,fr-hex.msh -dataelsetcol lightblue -showelt1d all -dataelt1drad 0.004 -dataelt3dedgerad 0.0022 -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 600:500 -cameraangle 24 -print fr-hex
$ convert +append fr-cub.png fr-hex.png fr4.png
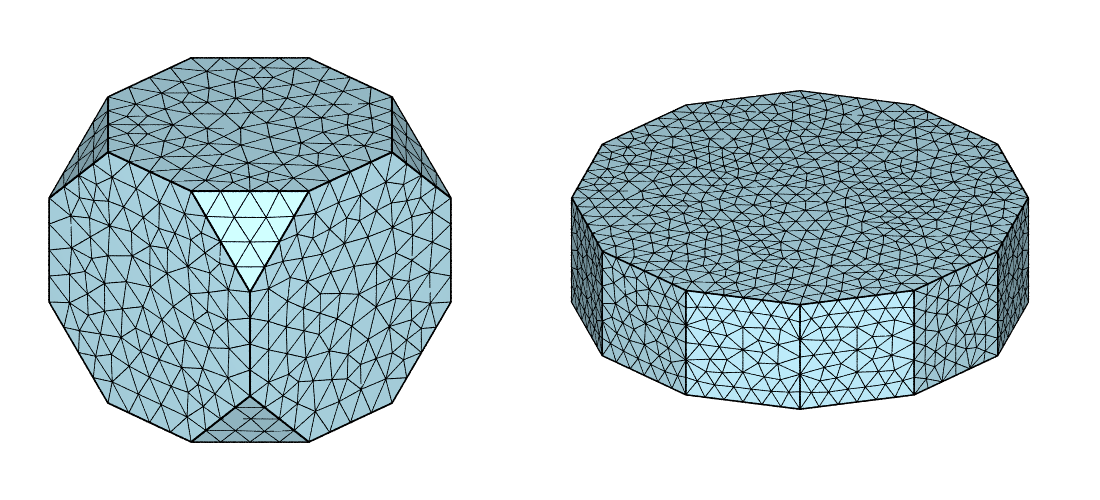
Optionally, the frontal 2D meshing algorithm can be enforced to generate a more regular surface mesh:
$ neper -M fr-cub.tess -cl 0.1 -mesh2dalgo fron
$ neper -M fr-hex.tess -cl 0.1 -mesh2dalgo fron
$ neper -V fr-cub.tess,fr-cub.msh -dataelsetcol lightblue -showelt1d all -dataelt1drad 0.003 -dataelt3dedgerad 0.0015 -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 500:500 -cameraangle 13 -print fr-cub
$ neper -V fr-hex.tess,fr-hex.msh -dataelsetcol lightblue -showelt1d all -dataelt1drad 0.004 -dataelt3dedgerad 0.0022 -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 600:500 -cameraangle 24 -print fr-hex
$ convert +append fr-cub.png fr-hex.png fr5.png
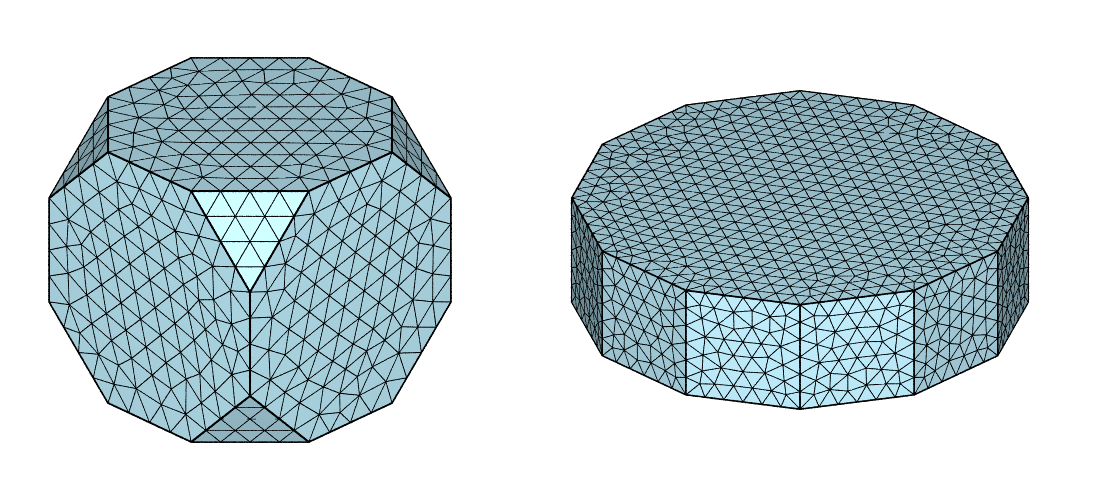
Note
Such meshes can be used in -orispace, in the Simulation Module (-S).
Generating and Meshing a Periodic Fundamental Region
Note
This is available only for 1-cell tessellations (-n1).
Periodicity can be enforced using -periodicity1 (-per 1 for short):
$ neper -T -n 1 -domain "rodrigues(cubic)" -per 1 -o fr-cub
$ neper -T -n 1 -domain "rodrigues(hexagonal)" -per 1 -o fr-hex
which visually does not change anything at all:
$ neper -V fr-cub.tess -datacellcol lightblue -datacelltrs 0.5 -dataedgerad 0.003 -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 500:500 -cameraangle 13 -print fr-cub
$ neper -V fr-hex.tess -datacellcol lightblue -datacelltrs 0.5 -dataedgerad 0.004 -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 600:500 -cameraangle 24 -print fr-hex
$ convert +append fr-cub.png fr-hex.png fr6.png
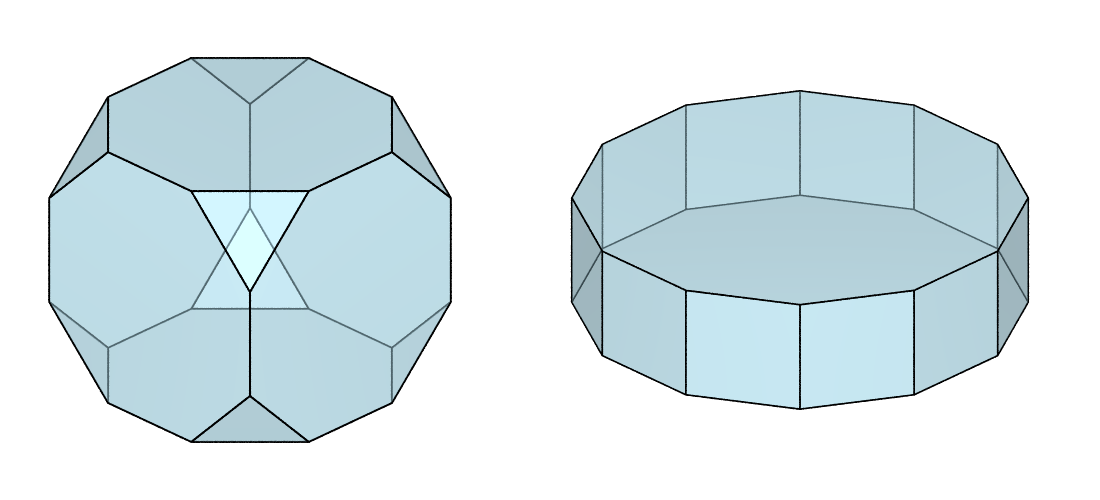
However, this defines periodicity relationships for the vertices, edges and faces in the Tessellation File (.tess).
The generated tessellations can be meshed:
$ neper -M fr-cub.tess -cl 0.1 -mesh2dalgo fron
$ neper -M fr-hex.tess -cl 0.1 -mesh2dalgo fron
$ neper -V fr-cub.tess,fr-cub.msh -dataelsetcol lightblue -showelt1d all -dataelt1drad 0.003 -dataelt3dedgerad 0.0015 -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 500:500 -cameraangle 13 -print fr-cub
$ neper -V fr-hex.tess,fr-hex.msh -dataelsetcol lightblue -showelt1d all -dataelt1drad 0.004 -dataelt3dedgerad 0.0022 -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 600:500 -cameraangle 24 -print fr-hex
$ convert +append fr-cub.png fr-hex.png fr7.png
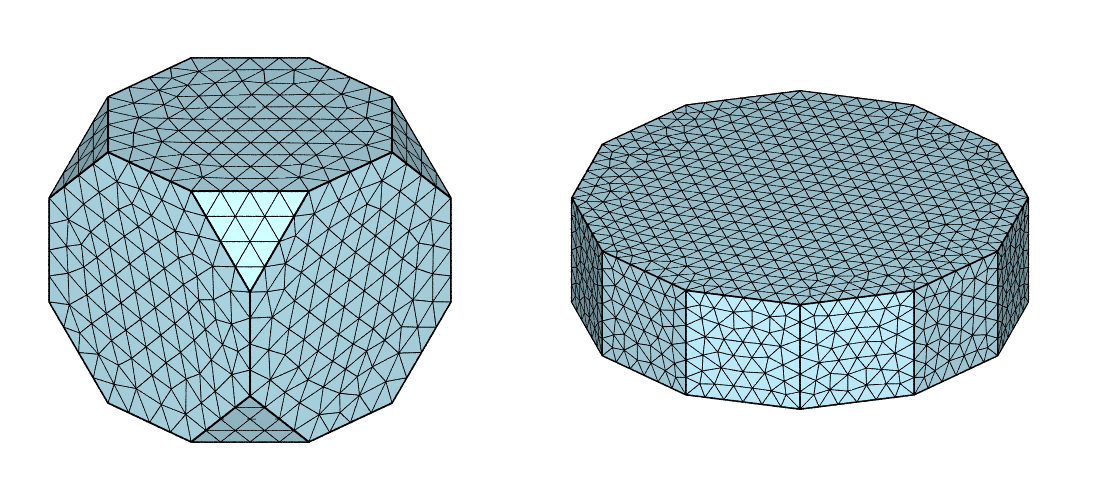
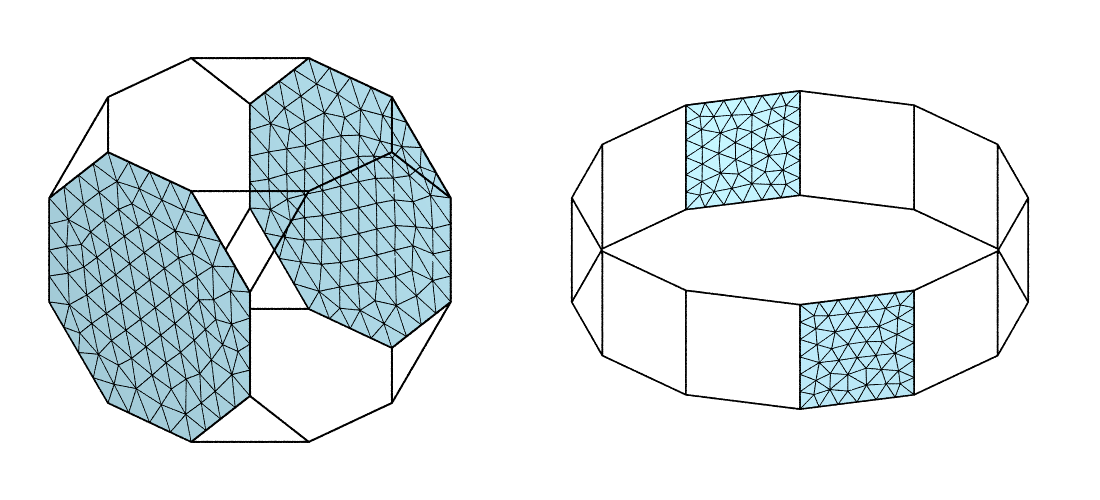
The meshes of the opposite faces, which can be visualized as follows, are such that their nodes follow the orientation equivalency [1]:
$ neper -V fr-cub.tess,fr-cub.msh -showelt3d none -showelt2d "elset2d<=2" -dataelt2dcol lightblue -showelt1d all -dataelt1drad 0.003 -dataelt2dedgerad 0.0015 -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 500:500 -cameraangle 13 -print fr-cub
$ neper -V fr-hex.tess,fr-hex.msh -showelt3d none -showelt2d "elset2d==9||elset2d==10" -dataelt2dcol lightblue -showelt1d all -dataelt1drad 0.004 -dataelt2dedgerad 0.0022 -cameracoo 4:4:3 -cameraprojection orthographic -imagesize 600:500 -cameraangle 24 -print fr-hex
$ convert +append fr-cub.png fr-hex.png fr8.png