Expressions and Keys

Mathematical and Logical Expressions

Neper handles mathematical expressions thanks to the muparser library. The expression must contain no space, tabulation or new-line characters, and match the following syntax. [1]

Functions

The following table gives an overview of the functions supported by the default implementation. It lists the function names, the number of arguments and a brief description.

Name	Description
sin	sine function
cos	cosine function
tan	tangens function
asin	arcus sine function
acos	arcus cosine function
atan	arcus tangens function
sinh	hyperbolic sine function
cosh	hyperbolic cosine
tanh	hyperbolic tangens function
asinh	hyperbolic arcus sine function
acosh	hyperbolic arcus tangens function
atanh	hyperbolic arcur tangens function
log2	logarithm to the base 2
log10	logarithm to the base 10
log	logarithm to the base 10
ln	logarithm to base \(e\) (2.71828…)
exp	e raised to the power of x
sqrt	square root of a value
sign	sign function: -1 if \(x<0\); 1 if \(x>0\)
rint	round to nearest integer
abs	absolute value
min	min of all arguments
max	max of all arguments
sum	sum of all arguments
avg	mean value of all arguments

Binary Operators

The following table lists the default binary operators supported by the parser.

Operator	Description	Priority
&&	logical and	1
||	logical or	2
<=	less or equal	4
>=	greater or equal	4
!=	not equal	4
==	equal	4
>	greater than	4
<	less than	4
+	addition	5
-	subtraction	5
*	multiplication	6
/	division	6
^	raise x to the power of y	7

Ternary Operators

The parser has built in support for the if-then-else operator. It uses lazy evaluation in order to make sure only the necessary branch of the expression is evaluated.

Operator	Description
?:	if-then-else operator, following the C/C++ syntax: (<test>)?<value_if_true>:<value_if_false>.

Statistical Distributions

The following table lists the statistical distributions. Custom endpoints (not indicated) can also be added as arguments, as described in the following.

Operator	Description	Information
normal(<mean>,<sigma>)	normal
lognormal(<mean>,<sigma>)	lognormal
dirac(<mean>)	Dirac
beta(<x>,<y>)	beta function	\(x>0\), \(y>0\)
lorentzian(<mean>,<sigma>)	Lorentzian
studentst(<mean>,<sigma>)	Student’s t
weibull(k,<sigma>)	Weibull	\(k > 0\) represents the shape
breitwigner(<mean>,<sigma>[,<gamma>])	Breit-Wigner	\(<gamma> \geq 0\), default 1
expnormal(<mean>,<sigma>[,<gamma>])	exp-normal	\(<gamma> > 0\), default \(<sigma>\)
moffat(<mean>,<sigma>[,<gamma>])	Moffat	\(<gamma> > 0\), default 1
pearson7(<mean>,<sigma>[,<gamma>])	Pearson type VII	default \(<gamma> = 1.5\)
pseudovoigt(<mean>,<sigma>[,<gamma>])	Pseudo-Voigt	\(<gamma> \in [0,\,1]\), default 0.5
skewnormal(<mean>,<sigma>[,<gamma>])	skewed normal	default \(<gamma> = <sigma>\)
custom(<file_name>)	custom

<mean> represents the mean (or centre), and <sigma> represents the standard deviation (or scale, \(> 0\)). <gamma> depends on the distribution function (see the above table). For all distributions but weibull and beta, custom endpoints can be added as last arguments, as <from_value>,<to_value>, where <from_value> is the lower endpoint and <to_value> is the upper endpoint. The parameter keywords do not need to be provided, but, when they are, the parameters can be given in any order, as in moffat(gamma=1,from=0,to=1,sigma=0.1,mean=0.5). Endpoints are considered inclusive by default, but exclusive endpoints can be specified using fromexclusive=<from_value> and toexclusive=<to_value> (frominclusive=<from_value> and toinclusive=<to_value> can be used for inclusive endpoints). String completion is available for the keywords. Finally, a sum of distributions of increasing averages can be provided, as in 0.3*lognormal(0.5,0.1)+0.7*normal(1,0.1).

Attention

When from and/or to are used, they should preferably be so that the distribution retains the same mean; otherwise, the distribution is shifted after truncation to match the specified mean.

In the case of the custom distribution, the numerical distribution must be provided in the file. The file must contain the x and y values of the distribution on successive lines. The x values must be provided in ascending order and form a regular grid. The distribution must contain at least 3 points and does not need to integrate to 1.

Tessellation Keys

Available keys for a tessellation itself are provided below.

Key	Descriptor	Apply to
dim	dimension	tess
vernb	number of vertices	tess
edgenb	number of edges	tess
facenb	number of faces	tess
polynb	number of polyhedra	tess
cellnb	number of cells	tess
x	x coordinate	tess
y	y coordinate	tess
z	z coordinate	tess
coo	x, y and z coordinates	tess
area	surface area	tess
vol	volume	tess
size	size (surface area/volume in 2D/3D)	tess
step	simulation step	tess

Available keys for tessellation seeds, vertices, edges, faces, polyhedra, crystals and cell groups are provided below. Also note that the keys apply to cells if they are tagged to apply to polyhedra and the tessellation is 3D and faces and the tessellation is 2D, and that keys apply to crystals if they apply to cells. You may also replace, in the tessellation keys themselves, poly by cell if the tessellation is 3D and face by cell if the tessellation is 2D (it applies only in rare cases). For example, for a 2D tessellation, you may use -statcell ncells instead of -statface nfaces. Keys specific to cells are defined accordingly in the following but also apply to polys is the tessellation is 3D and faces is the tessellations is 2D.

To turn a key value into a value relative to the mean over all entities (e.g. the relative cell size), append the key expression with the :rel modifier. To turn a key value into a value which holds for a unit cell size, append the key expression with the :uc modifier. To use as a reference only the body entities (see below), append b to the modifiers.

Key	Descriptor	Apply to
id	identifier	seed, ver, edge, face, poly, group
x	x coordinate	seed, ver, edge, face, poly
y	y coordinate	seed, ver, edge, face, poly
z	z coordinate	seed, ver, edge, face, poly
coo	x, y and z coordinates	seed, ver, edge, face, poly
xmin	minimum x coordinate	edge, face, poly
ymin	minimum y coordinate	edge, face, poly
zmin	minimum z coordinate	edge, face, poly
xmax	maximum x coordinate	edge, face, poly
ymax	maximum y coordinate	edge, face, poly
zmax	maximum z coordinate	edge, face, poly
w	weight (width for a lamellar tessellation)	seed, cell
body[<expr>]	body level	ver, edge, face, poly
state	state	ver, edge, face, poly
domtype	type of domain (0 if on a domain vertex, 1 if on a domain edge and 2 if on a domain face)	ver, edge, face
domface	domain face (-1 if undefined)	face
domedge	domain edge (-1 if undefined)	edge
domver	domain vertex (-1 if undefined)	ver
scale	scale	ver, edge, face, poly, cell [2]
length	length	edge
length(<d_x>,<d_y>,<d_z>)	directional length along \((d_x,d_y,d_z)\) (in 2D, d_z can be omitted)	edge, face, poly
area	surface area	face, poly, group
vol	volume	poly, group
size	size (surface area/volume in 2D/3D)	cell, group
diameq	equivalent diameter [4]	face, poly
avdiameq	average equivalent diameter [4]	face, poly
radeq	equivalent radius (half of the eq. diameter)	face, poly
avradeq	average equivalent radius (half of the eq. diameter)	face, poly
sphericity	sphericity [5]	poly
circularity	circularity [6]	face
convexity	convexity [7]	face (only for a 2D tessellation), poly
dihangleav	average dihedral angle	face, poly
dihanglemin	minimum dihedral angle	face, poly
dihanglemax	maximum dihedral angle	face, poly
dihangles	dihedral angles	face, poly
ff	flatness fault (in degrees)	face
theta	disorientation angle (in degrees)	edge (in 2D), face (in 3D)
cyl	cylinder polygonization [19]	edge
vernb	number of vertices	edge, face, poly
vers	vertices	edge, face, poly
edgenb	number of edges	ver, face, poly
edges	edges	ver, face, poly
facenb	number of faces	ver, edge, poly
faces	faces	ver, edge, poly
polynb	number of polyhedra	ver, edge, face
polys	polyhedra	ver, edge, face
nfacenb	number of neighboring faces	face
nfaces	neighboring faces	face
nfacenb_samedomain	number of neighboring faces of the same domain (parent cell of a multiscale tessellation)	face (in 2D)
nfaces_samedomain	neighboring faces of the same domain (parent cell of a multiscale tessellation)	face (in 2D)
npolynb	number of neighboring polyhedra	poly
npolys	neighboring polyhedra	poly
npolys_unsort	neighboring polyhedra, unsorted list	poly
npolynb_samedomain	number of neighboring polyhedra of the same domain (parent cell of a multiscale tessellation)	poly
npolys_samedomain	neighboring polyhedra of the same domain (parent cell of a multiscale tessellation)	poly
vercoos	vertex coordinates	face, poly
faceareas	face surface areas	poly
faceeqs	face equations [9]	poly
nseednb	number of neighboring seeds	poly
nseeds	neighboring seeds [10]	poly
scaleid(<scale_nb>)	identifier of the corresponding cell at scale <scale_nb>	cell
lam	lamella width id [11]	cell
mode	mode [12]	cell
group	group	cell
per	periodic (1 if periodic, 0 otherwise)	ver, edge, face (in 3D)
fiber(...)	1 if in orientation fiber and 0 otherwise, see Orientation Fibers	poly
<orientation_descriptor>	orientation descriptor	face (in 2D), poly (in 3D)
step	simulation step	ver, edge, face, poly

Variables consisting of several values (vers, etc.) are not available for sorting (option -sort).

For a cell, the body variable is defined as follows:

• In the general case (body, no argument provided), it is an integer equal to 0 if the cell is at the domain boundary, i.e. if it shares at least one face with it (edge in 2D), and is equal to 1 or higher otherwise. This is determined as follows: if a cell is surrounded by cells with body values equal to or higher than n, its body value is equal to n + 1. Therefore, body tends to increase with the distance to the domain boundary and can be used to define cells that may suffer from boundary effects.

• In the case where an expression is provided as argument (body(<expr>)), the expression is a logical expression that defines the boundary to consider, from the domain face (edge in 2D) labels (for a cube, x0, x1, y0, y1, z0 and z1). For example, body(z0||z1) considers only the z0 and z1 domain faces as the boundary, and the more exotic body(x1&&y0||z1) considers only the intersection between the x1 and y0 domain faces, and the z1 domain face as the boundary.

For entities of lower dimension than cells (vertices, edges and faces), body is equal to the maximum body value of the cells they belong to.

Raster Tessellation Keys

Available keys for raster tessellation itself are provided below.

Key	Descriptor	Apply to
dim	dimension	tesr
voxnbx	number of voxels in direction x	tesr
voxnby	number of voxels in direction y	tesr
voxnbz	number of voxels in direction z	tesr
voxnb	number of voxels in total	tesr
originx	origin x coordinate	tesr
originy	origin y coordinate	tesr
originz	origin z coordinate	tesr
voxsizex	voxel size in direction x	tesr
voxsizey	voxel size in direction y	tesr
voxsizez	voxel size in direction z	tesr
rastersizex	raster size in direction x	tesr
rastersizey	raster size in direction y	tesr
rastersizez	raster size in direction z	tesr
rastersize	raster size (surface area/volume in 2D/3D)	tesr
area	surface area	tesr
vol	volume	tesr
size	size (surface area/volume in 2D/3D)	tesr
x	x coordinate	tesr
y	y coordinate	tesr
z	z coordinate	tesr
coo	x, y and z coordinates	tesr
step	simulation step	tesr

Available keys for raster tessellation seeds, cells, cell groups and voxels are provided below. Mathematical and logical expressions based on these keys can also be used. To turn a key value into a value relative to the mean over all entities (e.g.the relative cell size), append the key expression with the :rel modifier. To turn a key value into a value which holds for a unit cell size, append the key expression with the :uc modifier.

General

Key	Descriptor	Applies to
id	identifier	seed, cell, group, voxel
cell	cell	voxel
oridef	orientation is defined	voxel
w	Laguerre weight	seed
step	simulation step	tesr

Geometry

Key	Descriptor	Applies to
x	x coordinate	seed, cell, voxel
y	y coordinate	seed, cell, voxel
z	z coordinate	seed, cell, voxel
coo	x, y and z coordinates	seed, cell, voxel
vx	x coordinate (in voxel)	voxel
vy	y coordinate (in voxel)	voxel
vz	z coordinate (in voxel)	voxel
vcoo	x, y and z coordinates (in voxel)	voxel
vxmin	minimum x coordinate (in voxel)	cell
vymin	minimum y coordinate (in voxel)	cell
vzmin	minimum z coordinate (in voxel)	cell
vxmax	maximum x coordinate (in voxel)	cell
vymax	maximum y coordinate (in voxel)	cell
vzmax	maximum z coordinate (in voxel)	cell
domvxmin	domain minimum x coordinate (in voxel), always 1	domain
domvymin	domain minimum y coordinate (in voxel), always 1	domain
domvzmin	domain minimum z coordinate (in voxel), always 1	domain
domvxmax	domain maximum x coordinate (in voxel)	domain
domvymax	domain maximum y coordinate (in voxel)	domain
domvzmax	domain maximum z coordinate (in voxel)	domain
area	surface area	cell, group (in 2D)
vol	volume	cell, group (in 3D)
size	size (surface area/volume in 2D/3D)	cell, group
voxnb	number of voxels	cell
areafrac	surface area fraction	group (in 2D)
volfrac	volume fraction	group (in 3D)
sizefrac	size fraction (surface area/volume fraction in 2D/3D)	group
diameq	equivalent diameter [4]	cell
radeq	equivalent radius	cell
convexity	convexity [7]	cell

Orientation

Key	Descriptor	Applies to
<orientation_descriptor>	orientation descriptor	voxel, cell
gos	grain orientation spread [8]	cell
oridisanisoangles	orientation distribution anisotropy / principal angles [13]	cell
oridisanisoaxes	orientation distribution anisotropy / principal axes [13]	cell
oridisanisofact	orientation distribution anisotropy factor [13]	cell
oridisanisodeltas	orientation distribution anisotropy / principal delta angles [14]	cell

Tessellation Optimization Keys

Time Keys

The available keys for option -morphooptilogtime are provided below. Use iter(<factor>), where factor is an integer reduction factor, to log values only at specific iteration numbers.

Key	Descriptor
iter	iteration number
varupdateqty	number of updated variables
seedupdateqty	number of updated seeds
seedupdatelist	list of updated seeds
cellupdateqty	number of updated cells
cellupdatelist	list of updated cells
var	time for variable update
seed	time for seed update
cell_init	time for cell update initialization
cell_kdtree	time for cell update kdtree computation
cell_shift	time for cell update shift computation
cell_neigh	time for cell update neighbor computation
cell_cell	time for cell update cell computation
cell_other	time for cell update others
cell_total	total time for cell update
val	time for (objective function) value update
val_init	time for (objective function) value update / initialization
val_penalty	time for (objective function) value update / penalty computation
val_val	time for (objective function) value update / value computation
val_val_cellval	time for (objective function) value update / value computation / cell values
val_val_comp	time for (objective function) value update / value computation / computation
val_comp	time for (objective function) value update / computation
total	total time
cumtotal	cumulative total time

Variable Keys

The available keys for option -morphooptilogvar are provided below. Use iter(<factor>), where factor is an integer reduction factor, to log values only at specific iteration numbers.

Key	Descriptor	Apply to
iter	iteration number	n/a
id	identifier	seed
x	x coordinate	seed
y	y coordinate	seed
z	z coordinate	seed
w	weight	seed

Objective Function Value Keys

The available keys for option -morphooptilogval are provided below. Use iter(<factor>), where factor is an integer reduction factor, to log values only at specific iteration numbers.

Key	Descriptor
iter	iteration number
val	value
valmin	minimal value
val0	value, without smoothing
valmin0	minimal value, without smoothing
val(<i>)	i th subvalue
val0(<i>)	i th subvalue, without smoothing
eps	error on the objective function (see -morphooptistop)
reps	relative error on the objective function (see -morphooptistop)
loop	optimization loop
plateaulength	current plateau length [15]

Statistical Distribution Keys

The available keys for option -morphooptilogdis are provided below. PDF stands for probability density function and CDF stands for cumulative probability density function. Use iter(<factor>), where factor is a reduction factor, to log values only at specific iteration numbers.

Key	Descriptor
iter	iteration number
x	x coordinate
tarpdf	target PDF
tarcdf	target CDF
curpdf	current PDF
curcdf	current CDF
tarpdf0	target PDF, not smoothed
tarcdf0	target CDF, not smoothed
curcdf0	current CDF, not smoothed

Raster Tessellation Voxel Keys

The available keys for option -morphooptilogtesr are provided below. Values are written for each voxel used to compute the objective function. Use iter(<factor>), where factor is a reduction factor, to log values only at specific iteration numbers.

Key	Descriptor
iter	iteration number
id	cell identifier
x	x coordinate
y	y coordinate
z	z coordinate
dist	distance to the cell

Orientation Optimization Keys

Variable Keys

The available keys for option -orioptilogvar are provided below. For all orientation descriptors but quaternion, the returned orientation are located in the fundamental region. Use iter(<factor>), where factor is an integer reduction factor, to log values only at specific iteration numbers.

Key	Descriptor	Apply to
iter	iteration number	n/a
id	identifier	seed
rodrigues	Rodrigues vector	seed
euler-bunge	Euler angles (Bunge convention)	seed
euler-kocks	Euler angles (Kocks convention)	seed
euler-roe	Euler angles (Roe convention)	seed
rotmat	Rotation matrix	seed
axis-angle	rotation axis / angle pair	seed
quaternion	quaternion	seed

Mesh Keys

Available keys for a mesh itself are provided below. “co” stands for “cohesive”.

Key	Descriptor	Apply to
eltnb	element number	{0-3}D,co mesh
nodenb	node number	{0-3}D mesh
elsetnb	elset number	{0-3}D,co mesh
partnb	partition number	highest-dimension mesh
x	x coordinate	{0-3}D mesh
y	y coordinate	{0-3}D mesh
z	z coordinate	{0-3}D mesh
coo	x, y and z coordinates	{0-3}D mesh
length	length	1D mesh
area	surface area	2D mesh
vol	volume	3D mesh
size	size (length/area/volume in 1D/2D/3D)	{1-3}D mesh
step	simulation step	{0-3}D,co mesh

Available keys for mesh node, elements and element sets (of all dimensions) and points are provided below. “co” stands for “cohesive”.

Key	Descriptor	Apply to
id	identifier	node, {0-3}D,co elt, {0-3}D,co elset
x	x coordinate	node, {0-3}D,co elt, {0-3}D elset
y	y coordinate	node, {0-3}D,co elt, {0-3}D elset
z	z coordinate	node, {0-3}D,co elt, {0-3}D elset
coo	x, y and z coordinates	node, {0-3}D,co elt, {0-3}D elset
dim	lowest parent elt dimension	node
elset0d	0D elset	0D elt
elset1d	1D elset	1D elt
elset2d	2D elset	2D elt
elset3d	3D elset	3D elt
elsetco	Cohesive elset	co elt
part	partition	{0-3}D elt, node
group	group	{0-3}D elt, {0-3}D elset
scaleid(<scale_nb>)	identifier of the corresponding tess cell at scale <scale_nb>	2D elset, 3D elset
scale	scale	{0-2}D elset [3]
cyl	cylinder polygonization [19]	1D elt, 1D elset
vol	volume	3D elt, 3D elset
vol_orispace	volume, orientation-space-wise [20]	3D elt
area	surface area	2D elt
diameq	equivalent diameter	{2,3}D elt, {2,3}D elset
radeq	equivalent radius	{2,3}D elt, {2,3}D elset
length	average edge length	{0-3}D elt, 1D elset
lengths	edge lengths	2D elt, 3D elt
elsetvol	elset volume	3D elt
elsetarea	elset area	2D elt
elsetlength	elset length	1D elt
rr	radius ratio	3D elt
rrav	average radius ratio	3D elset
rrmin	min radius ratio	3D elset
rrmax	max radius ratio	3D elset
Osize	Osize	3D elset
eltnb	number of elements	{0-3}D,co elset
elts	elements	{0-3}D,co elset
nodenb	number of nodes	{0-3}D,co elset
nodes	nodes	{0-3}D,co elset
body	body level	{0-3}D elt, {0-3}D elset
elsetbody	body level, relative to the elset boundary	{1-3}D elt
domtype	type of domain [16]	{0-2}D elt, {0-2}D elset
2dmeshp	closest point of the 2D mesh	node, 3D elt
2dmeshd	distance to 2dmeshp	node, 3D elt
2dmeshv	vector to 2dmeshp	node, 3D elt
2dmeshn	outgoing normal vector at 2dmeshp	node, 3D elt
per	periodic (1 if periodic, 0 otherwise)	{0,1}D elt, 2D elt (in 3D), {0,1}D elset, 2D elset (in 3D)
col_rodrigues	color in Rodrigues vector convention [17]	node
col_stdtriangle	color in IPF convention, cubic symmetry [18]	node
col_stdtriangle_hexagonal	color in IPF convention, hexagonal symmetry [18]	node
fiber(...) [21]	1 if in orientation fiber and 0 otherwise	3D elt, 3D elset
theta	disorientation angle (in degrees)	1D elt and elset (in 2D), 2D elt and elset (in 3D)
gos	grain orientation spread [8]	{2,3}D elset
anisogos	grain orientation spread estimated from the orientation distribution	[8] {2,3}D elset
<orientation_descriptor>	orientation descriptor	2D elt (in 2D), 2D elset (in 2D), 3D elt (in 3D), 3D elset (in 3D)
step	simulation step	{0-3}D,co mesh

Variables beginning with 2dmesh are only available for statistics (options beginning with -stat of module -M); for elements, they apply to the centroids.

Point Keys

Available keys for points are provided below.

Key	Descriptor	Apply to	Require
id	identifier	point
x	x coordinate	point
y	y coordinate	point
z	z coordinate	point
cell	cell	point	tessellation
elt	containing element	point	mesh
elset	containing elset	point	mesh
2dmeshp	coordinates of the closest point of the 2D mesh	point	3D mesh
2dmeshd	distance to 2dmeshp	point	3D mesh
2dmeshv	vector to 2dmeshp	point	3D mesh
2dmeshn	outgoing normal vector of the 2D mesh at 2dmeshp	point	3D mesh

Simulation Results

A result of a Simulation Directory (.sim) can be invoked simply from its name. A component of a vectorial or tensorial result can be invoked by prefixing the component to the name, as in coo1, stress11, etc. For a symmetrical tensor (for which only 6 values are stored), t, both t<i><j> and t<j><i> are valid. The type of a result of the simulation directory is determined automatically. Tessellation results can be obtained from the cell results, by averaging or other statistical treatments. Similarly, elset and mesh results can be obtained from the element results, by averaging or other statistical treatments.

Available results / keys for nodes are the following:

Key	Descriptor	Apply to
disp	displacement (computed from positions)	node

Available results / keys for elements sets are the following:

Key	Descriptor	Apply to
ori	average orientation	elset, mesh
gos	grain orientation spread [8]	elset
anisogos	grain orientation spread computed from oridisanisoangles	elset
oridisanisoangles	orientation distribution principal angles	elset, mesh
oridisanisoaxes	orientation distribution principal axes	elset, mesh
oridisanisofact	orientation distribution factor	elset, mesh
odf(<var>=<value>,...)	ODF defined at elements of orientation space (see also below)	tess, tesr, mesh, cell, elt, elset
odfn(<var>=<value>,...)	ODF defined at nodes of orientation space (see also below)	tess, tesr, mesh
orifield(var=<var>,...)	<var> field defined at elements of orientation space (see below)	mesh
orifieldn(var=<var>,...)	<var> field defined at nodes of orientation space (see below)	mesh

The ODF (odf or odfn) of a tessellation or mesh is computed over orientation space (provided using -orispace) from the orientations of the (tessellation) cells or (mesh) elsets. The (optional) parameters are:

• input: the input used for the orientations, either elsets or elts for a mesh (default elsets);

• theta: the standard deviation of the kernel (in degrees);

• weight: the weight of a cell or elset, which can be a real value or an expression based on the Tessellation Keys (for cells) or Mesh Keys (for elsets) – by default, the volumes of the cells or elsets are used;

• clustering: a logical value controlling orientation clustering, which can be 0 (for no clustering) or 1 (for clustering); the default is 0 for cells or elsets and 1 for voxels or elements;

• cutoff: the cut-off factor used to compute the ODF, which can be all (for no cut-off) or any positive real value (default 5).

For a cell, element or elset, odf returns the value of the ODF of the tessellation or mesh at the corresponding orientation (and simulation step).

The orifield and orifieldn of a mesh is computed over orientation space (provided using -orispace) from the values of the (mesh) elsets. The mandatory parameter is:

• var: the variable, which must be defined for elsets (i.e., have its files in the simulation directory);

and the optional parameters are:

• theta: the standard deviation of the kernel (in degrees);

• weight: the weight of an elset, which can be a real value or an expression based on the Mesh Keys (for elsets) – by default, the volumes of the elsets are used.

Rotations and Orientations

Rotation and Orientation Descriptors

Rotations and orientations can be described using the following descriptors.

Key	Descriptor	Number of parameters
rodrigues	Rodrigues vector	3
euler-bunge	Euler angles (Bunge convention)	3
euler-kocks	Euler angles (Kocks convention)	3
euler-roe	Euler angles (Roe convention)	3
rotmat	rotation matrix	9
axis-angle	rotation axis / angle pair	4
quaternion	quaternion	4

The convention can be added to the descriptor, either active or passive, as in rodrigues:active. When no convention is provided, passive is assumed.

Some options can take parameter values as argument, in which case the orientation must be expressed as <descriptor>(<parameter1>,<parameters2>,...). An example is rodrigues(0.1,0.2,0.3).

Orientation Convention

The crystal coordinate systems are attached to the crystal lattice as illustrated below, in the case of cubic and hexagonal symmetries:

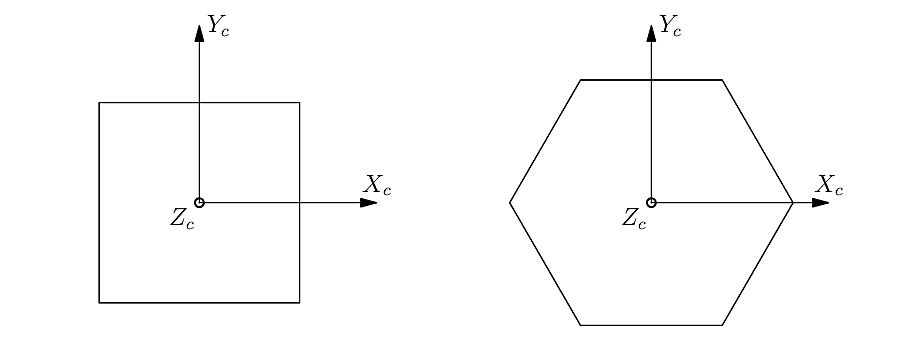
The so-called “passive” orientation convention is used by default, which is based on the rotation of the sample coordinate system into the crystal coordinate system. Under this convention, the values of all Rotation and Orientation Descriptors are provided below for a simple (but representative) configuration that corresponds to a rotation of 30° about \(X_s\):

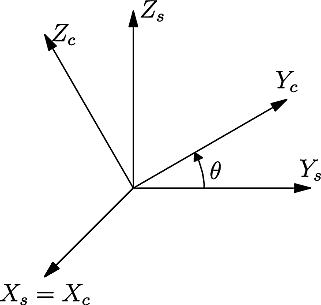
Descriptor	Value (angles in degrees)
Rodrigues vector	\((0.267949192,\,0,\,0)\)
Euler angles (Bunge convention)	\((0,\,30,\,0)\)
Euler angles (Kocks convention)	\((270,\,30,\,90)\)
Euler angles (Roe convention)	\((270,\,30,\,90)\)
rotation matrix	\(\left(\begin{array}{ccc}1 & 0 & 0 \\ 0 & 0.866025404 & 0.5 \\ 0 & -0.5 & 0.866025404\\\end{array}\right)\)
rotation axis / angle pair	\((1,\,0,\,0) / 30\)
quaternion	\((0.965925826,\,0.258819045,\,0,\,0)\)

The values of the orientation descriptors under the “active” convention are obtained by taking the opposite rotation.

Ideal Orientations

Keys are available for ideal orientations (lowercased is accepted):

Key	Miller indices
Cube	\((0\,0\,1)[1\,0\,0]\)
Goss	\((0\,1\,1)[1\,0\,0]\)
U	\((1\,0\,1)[\overline{1}\,0\,1]\)
45NDCube	\((0\,0\,1)[1\,\overline{1}\,0]\)
S1	\((1\,2\,3)[6\,3\,\overline{4}]\)
S2	\((\overline{1}\,2\,3)[6\,\overline{3}\,4]\)
S3	\((1\,\overline{2}\,3)[6\,\overline{3}\,\overline{4}]\)
S4	\((\overline{1}\,\overline{2}\,3)[6\,3\,4]\)
Brass1	\((1\,1\,0)[1\,\overline{1}\,2]\)
Brass2	\((\overline{1}\,1\,0)[1\,1\,\overline{2}]\)
Copper1	\((1\,1\,2)[1\,1\,\overline{1}]\)
Copper2	\((\overline{1}\,1\,2)[1\,\overline{1}\,1]\)

When loading orientations from an external file, use file(<file_name>[,des=<descriptor>]) where the orientation descriptor is among those listed above and is rodrigues:passive by default.

Orientation Fibers

Orientation fibers are defined by a crystal direction being parallel to a sample direction. Depending on the context, an angular tolerance or distribution with respect to the theoretical fiber can also be defined:

• fiber(<dirc_x>,<dirc_y>,<dirc_z>,<dirs_x>,<dirs_y>,<dirs_z>), where (<dirc_x>, <dirc_y>, <dirc_z>) is the crystal direction and (<dirs_x>, <dirs_y>, <dirs_z>) is the sample direction, corresponds to an ideal orientation fiber;

• fiber(<dirc_x>,<dirc_y>,<dirc_z>,<dirs_x>,<dirs_y>,<dirs_z>,<theta>), where <theta> is an angle expressed in degrees, corresponds to an orientation fiber with the angular tolerance <theta> from the ideal fiber;

• fiber(<dirc_x>,<dirc_y>,<dirc_z>,<dirs_x>,<dirs_y>,<dirs_z>):normal(<var>=<val>), where <var> can be theta or thetam) and <val> is the value, corresponds to an orientation fiber with a normal (Gaussian) disorientation normal to the ideal fiber.

Crystal Symmetries

Crystal symmetries can be described using the following descriptors.

Key	Descriptor	Number of operators
triclinic	triclinic (Laue group \(\overline{1}\))	24
cubic	cubic	24
hexagonal	hexagonal	1
-1	Laue group \(\overline{1}\)	1
2/m	Laue group \(2/m\)	2
mmm	Laue group \(mmm\)	4
4/m	Laue group \(4/m\)	4
4/mmm	Laue group \(4/mmm\)	8
-3	Laue group \(\overline{3}\)	3
-3m	Laue group \(\overline{3}m\)	6
6/m	Laue group \(6/m\)	6
6/mmm	Laue group \(6/mmm\)	12
m-3	Laue group \(m\overline{3}\)	12
m-3m	Laue group \(m\overline{3}m\)	24

Colors and Color Maps

Colors

The available colors are provided below, with their corresponding RGB channel values (ranging from 0 to 255). Any other color can be defined from the RGB channel values, under format <R_value>:<G_value>:<B_value>.

Key	RGB value
black	(0, 0, 0)
red	(255, 0, 0)
green	(0, 255, 0)
blue	(0, 0, 255)
yellow	(255, 255, 0)
magenta	(255, 0, 255)
cyan	(0, 255, 255)
white	(255, 255, 255)
maroon	(128, 0, 0)
navy	(0, 0, 128)
chartreuse	(127, 255, 0)
springgreen	(0, 255, 127)
olive	(128, 128, 0)
purple	(128, 0, 128)
teal	(0, 128, 128)
gray	(128, 128, 128)
deepskyblue	(0, 191, 255)
lawngreen	(124, 252, 0)
darkgray	(64, 64, 64)
orangered	(255, 69, 0)
silver	(192, 192, 192)
snow	(255, 250, 250)
darkred	(139, 0, 0)
darkblue	(0, 0, 139)
darkorange	(255, 140, 0)
azure	(240, 255, 255)
ghostwhite	(248, 248, 255)
ivory	(255, 255, 240)
mediumblue	(0, 0, 205)
lightpink	(255, 182, 193)
mintcream	(245, 255, 250)
indigo	(75, 0, 130)
lightcoral	(240, 128, 128)
pink	(255, 192, 203)
coral	(255, 127, 80)
salmon	(250, 128, 114)
floralwhite	(255, 250, 240)
aquamarine	(127, 255, 212)
lemonchiffon	(255, 250, 205)
gold	(255, 215, 0)
darkgreen	(0, 100, 0)
orange	(255, 165, 0)
aliceblue	(240, 248, 255)
lightcyan	(224, 255, 255)
lightyellow	(255, 255, 224)
darkmagenta	(139, 0, 139)
darkcyan	(0, 139, 139)
peru	(205, 133, 63)
steelblue	(70, 130, 180)
lavenderblush	(255, 240, 245)
seashell	(255, 245, 238)
mediumspringgreen	(0, 250, 154)
darkslateblue	(72, 61, 139)
darkgoldenrod	(184, 134, 11)
lightsalmon	(255, 160, 122)
bisque	(255, 228, 196)
lightskyblue	(135, 206, 250)
lightgoldenrodyellow	(250, 250, 210)
honeydew	(240, 255, 240)
cornsilk	(255, 248, 220)
peachpuff	(255, 218, 185)
whitesmoke	(245, 245, 245)
tomato	(255, 99, 71)
slategray	(112, 128, 144)
hotpink	(255, 105, 180)
oldlace	(253, 245, 230)
blanchedalmond	(255, 235, 205)
darkkhaki	(189, 183, 107)
moccasin	(255, 228, 181)
darkturquoise	(0, 206, 209)
mediumseagreen	(60, 179, 113)
mediumvioletred	(199, 21, 133)
violet	(238, 130, 238)
greenyellow	(173, 255, 47)
papayawhip	(255, 239, 213)
darkseagreen	(143, 188, 143)
rosybrown	(188, 143, 143)
deeppink	(255, 20, 147)
saddlebrown	(139, 69, 19)
darkviolet	(148, 0, 211)
dodgerblue	(30, 144, 255)
lightslategray	(119, 136, 153)
burlywood	(222, 184, 135)
navajowhite	(255, 222, 173)
linen	(250, 240, 230)
mediumslateblue	(123, 104, 238)
turquoise	(64, 224, 208)
skyblue	(135, 206, 235)
mediumturquoise	(72, 209, 204)
beige	(245, 245, 220)
mistyrose	(255, 228, 225)
tan	(210, 180, 140)
antiquewhite	(250, 235, 215)
thistle	(216, 191, 216)
limegreen	(50, 205, 50)
darksalmon	(233, 150, 122)
lightsteelblue	(176, 196, 222)
royalblue	(65, 105, 225)
palegreen	(152, 251, 152)
crimson	(220, 20, 60)
wheat	(245, 222, 179)
mediumorchid	(186, 85, 211)
lavender	(230, 230, 250)
khaki	(240, 230, 140)
lightgreen	(144, 238, 144)
paleturquoise	(175, 238, 238)
darkslategray	(47, 79, 79)
darkorchid	(153, 50, 204)
seagreen	(46, 139, 87)
yellowgreen	(154, 205, 50)
blueviolet	(138, 43, 226)
palevioletred	(219, 112, 147)
olivedrab	(107, 142, 35)
mediumpurple	(147, 112, 219)
sandybrown	(244, 164, 96)
darkolivegreen	(85, 107, 47)
mediumaquamarine	(102, 205, 170)
slateblue	(106, 90, 205)
palegoldenrod	(238, 232, 170)
forestgreen	(34, 139, 34)
midnightblue	(25, 25, 112)
lightseagreen	(32, 178, 170)
lightgray	(211, 211, 211)
orchid	(218, 112, 214)
cornflowerblue	(100, 149, 237)
sienna	(160, 82, 45)
firebrick	(178, 34, 34)
powderblue	(176, 224, 230)
indianred	(205, 92, 92)
dimgray	(105, 105, 105)
lightblue	(173, 216, 230)
chocolate	(210, 105, 30)
brown	(165, 42, 42)
goldenrod	(218, 165, 32)
gainsboro	(220, 220, 220)
plum	(221, 160, 221)
cadetblue	(95, 158, 160)

Color Maps

Color Map for Integer Values

The color map or palette used to represent integer values is defined from the above color list, by excluding colors of brightness below 0.2 and above 0.8. The brightness is defined as the average of the channel values divided by 255. The resulting list of colors is: (1) red, (2) green, (3) blue, (4) yellow, (5) magenta, (6) cyan, (7) chartreuse, (8) springgreen, (9) olive, (10) purple, (11) teal, (12) gray, (13) deepskyblue, (14) lawngreen, (15) darkgray, (16) orangered, (17) silver, (18) darkorange, (19) mediumblue, (20) indigo, (21) lightcoral, (22) coral, (23) salmon, (24) aquamarine, (25) gold, (26) orange, (27) darkmagenta, (28) darkcyan, (29) peru, (30) steelblue, (31) mediumspringgreen, (32) darkslateblue, (33) darkgoldenrod, (34) lightsalmon, (35) lightskyblue, (36) tomato, (37) slategray, (38) hotpink, (39) darkkhaki, (40) darkturquoise, (41) mediumseagreen, (42) mediumvioletred, (43) violet, (44) greenyellow, (45) darkseagreen, (46) rosybrown, (47) deeppink, (48) saddlebrown, (49) darkviolet, (50) dodgerblue, (51) lightslategray, (52) burlywood, (53) mediumslateblue, (54) turquoise, (55) skyblue, (56) mediumturquoise, (57) tan, (58) limegreen, (59) darksalmon, (60) lightsteelblue, (61) royalblue, (62) palegreen, (63) crimson, (64) mediumorchid, (65) khaki, (66) lightgreen, (67) darkslategray, (68) darkorchid, (69) seagreen, (70) yellowgreen, (71) blueviolet, (72) palevioletred, (73) olivedrab, (74) mediumpurple, (75) sandybrown, (76) darkolivegreen, (77) mediumaquamarine, (78) slateblue, (79) forestgreen, (80) midnightblue, (81) lightseagreen, (82) orchid, (83) cornflowerblue, (84) sienna, (85) firebrick, (86) indianred, (87) dimgray, (88) chocolate, (89) brown, (90) goldenrod, (91) plum and (92) cadetblue.

Color Maps for Real Values

The color map used to represent real values is smooth and obtained by interpolation between nominal colors. Tinycolormap is used to generate standard color maps, and the default is viridis. The color maps are

Key	Color bar
viridis
cividis
magma
inferno
plasma
parula
heat
hot
jet
gray
github

Alternatively, a custom color map can be provided as custom(<color1>,<color2>,...). Neper’s legacy color map (version \(< 4\)) is custom(blue,cyan,yellow,green) and can also be obtained using legacy:

legacy

Finally, it is possible to gradually fade the start of a color map, to make it starts with white. This can be done using the fade modifier, following the syntax <colormap>:fade[(threshold)]. The threshold ranges from 0 to 1 and is equal to 0.1 by default. Fading is applied linearly from 0 (full fading) to the threshold (no fading). Examples are show below:

viridis:fade
viridis:fade(0.2)

[1]

Taken from the muparser documentation

[2] (1,2)

Applies only to a 3D tessellation and relevant for multiscale tessellations. The scale of an entity (vertex, edge or face) is the scale at which the entity was created, and it ranges from 0 (for domain entities) to the number of scales of the tessellation (for the last created entities). The scale of a cell is determined based on the number of subcells of its parent cell.

[3]

Applies only to a 3D mesh and relevant for meshes of multiscale tessellations. The scale of an elset is equal to the scale of its corresponding tessellation entity [2].

[4] (1,2,3)

Equivalent diameter = diameter of the circle of equivalent area/volume in 2D/3D

[5]

Sphericity of a polyhedron = ratio of the surface area of the sphere of equivalent volume to the surface area of the polyhedron

[6]

Circularity of a polygon = ratio of the perimeter of the circle of equivalent area to the perimeter of the polygon

[7] (1,2)

Convexity of a polyhedron (face) = ratio of the volume (surface area) of the polyhedron (face) to the volume (surface area) of the convex hull of the polyhedron (face)

[8] (1,2,3,4)

Grain orientation spread = average disorientation (angle) with respect to the average orientation

[9]

A face equation is specified by the parameters \(d\), \(a\), \(b\) and \(c\), with the equation being: \(a x + b y + c z = d\). The vector \((a, b, c)\) is pointing outwards of the polyhedron.

[10]

If a polyhedron has no neighbor on a face, a negative value is returned.

[11]

In the case of a lamellar tessellation with several lamella widths, lam stands for the actual lamella width of the cell (starting from 1).

[12]

In the case of a multimodal tessellation (e.g.in terms of cell size), mode stands for the actual mode (starting from 1). Otherwise, it is equal to 1.

[13] (1,2,3)

R Quey, JH Driver, PR Dawson, Intra-grain orientation distributions in hot-deformed aluminium: orientation dependence and relation to deformation mechanisms, Journal of the Mechanics and Physics of Solids, vol. 84, pp. 506-524, 2015.

[14]

For Gaussian distributions, they are equal to 1.349 times the values of oridisanisoangles.

[15]

Number of iterations during which the objective function does not decrease

[16]

0 if on a domain vertex, 1 if on a domain edge and 2 if on a domain face

[17]

Applies to a mesh of Rodrigues space

[18] (1,2)

Applies to a mesh of the stereographic triangle

[19] (1,2)

1 if polygonize the circular part of a cylindrical domain and 0 otherwise.

[20]

For a mesh of orientation space (or a fundamental region), returns the volume in orientation space. Sums to \(\pi^2/n_c\), where \(n_c\) is the multiplicity of the orientation (24 for cubic symmetry).

[21]

See Orientation Fibers.