Generating a Tessellation from Statistical Cell Properties
Statistical morphological properties for the cells can be specified as input, using option -morpho. In this case, instead of a Voronoi tessellation, Neper generates a Laguerre tessellation (which can represent any tessellation comprised of convex cells, and therefore does not involve particular limitations) by optimizing the attributes of its seeds until the specified input is reached [CMAME2018].
Note
To reproduce exactly the images below, add the following line to your $HOME/.neperrc file (or to a local configuration file to be loaded with --rcfile):
neper -V -imagesize 800:400
Using the Built-in graingrowth
Option -morpho includes the graingrowth (or gg, for short) properties, which corresponds to those of an experimental polycrystal subjected to grain growth. Both the cell size distribution and the cell sphericity distribution (how close are the cells from a sphere) are defined [CMAME2018].
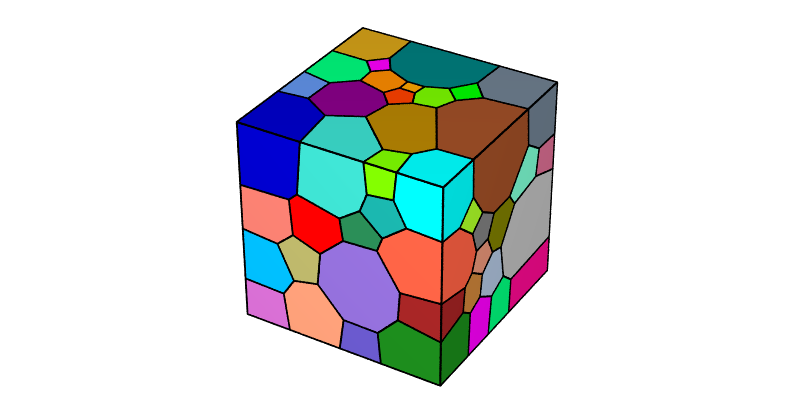
A 100-cell tessellation with grain-growth properties can be generated using the Tessellation Module (-T) as follows:
$ neper -T -n 100 -morpho gg
This produces a Tessellation File (.tess) named n100-id1.tess.
The tessellation can be visualized using the Visualization Module (-V):
$ neper -V n100-id1.tess -print img1
This produces a PNG file named img1.png.
Specifying Custom Properties
Statistical properties other than those of gg can be specified. gg actually is an alias for diameq:lognormal(1,0.35),1-sphericity:lognormal(0.145,0.03), where diameq::lognormal(1,0.35) specifies a lognormal distribution of the (normalized) cell equivalent diameters of average 1 and standard deviation 0.35, and 1-sphericity:lognormal(0.145,0.03) corresponds to a lognormal distribution of the cell “1-sphericities” of average 0.145 and standard deviation 0.03. It is therefore possible to use this longer argument and change the numerical values. For example, to get nearly equal-size cells (small standard deviation of the cell size lognormal distribution), one may use:
$ neper -T -n 100 -morpho "diameq:lognormal(1,0.05),1-sphericity:lognormal(0.145,0.03)"
The tessellation can be visualized as before:
$ neper -V n100-id1.tess -print img2

Of course, it is also possible to change the sphericity distribution, for instance to get less spherical grains (smaller average of the sphericity distribution):
$ neper -T -n 100 -morpho "diameq:lognormal(1,0.05),1-sphericity:lognormal(0.245,0.03)"
The tessellation can be visualized as before:
$ neper -V n100-id1.tess -print img3

Note
See Statistical Distributions for a list of possible distributions and other possible inputs.
Important
Although it is not strictly needed, distributions for both the sizes (e.g. diameq) and the shapes of the cells should be specified. Generating a tessellation from only a cell size distribution can lead to unrealistically small cell sphericities.
Specifying an Absolute Cell Size Distribution
It is possible to get Neper to consider the cell size distribution as a distribution of absolute values by using -n from_morpho (instead of an actual number of cells). Neper determines the number of cells from the cell size distribution and the domain size. An example is:
$ neper -T -n from_morpho -morpho "diameq:lognormal(0.2,0.06),1-sphericity:lognormal(0.145,0.03)" -o mytess
Note
Option -o is used to set the output file name. The default file name is n<n>-id<id>.tess and, in this case, would be the odd nfrom_morpho-id1.tess.
The tessellation contains 184 cells and can be visualized as before:
$ neper -V mytess.tess -print img4

Specifying an Experimental Cell Size Distribution
Experimental or, more generally, numerical distributions defined from a file can be specified by using option -morpho <property>:custom(<file_name>) (instead of analytical distributions).
Consider a cell-size (diameq) distribution defined from a file, mydistrib, that contains:
0.2 10.0
0.3 20.0
0.4 5.0
i.e., 10 cells have a diameq equal to 0.2, 20 cells have a diameq equal to 0.3, and 5 cells have a diameq equal to 0.4 (for a tessellation comprising 35 cells). The numbers on the right column are actually only considered relative to each other.
Note
In contrast to analytical distributions, numerical distributions do not need to be normalized to 1.
As for an analytical distribution, if
-morphofrom_morphois used, Neper determines the number of cells from the cell size distribution and the domain size.
The corresponding tessellation can be generated as follows:
$ neper -T -n from_morpho \
-morpho "diameq:custom(mydistrib),1-sphericity:lognormal(0.145,0.03)" \
-statcell diameq \
-o mytess
where option -statcell is used to output the cell equivalent diameters to file mytess.stcell.
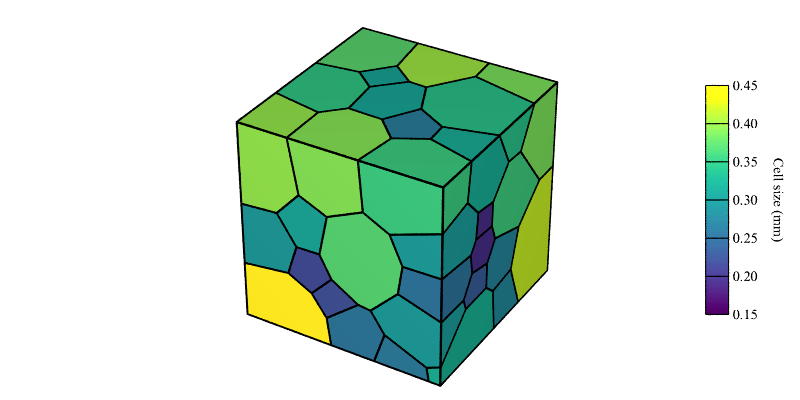
The tessellation can be visualized by coloring the cells from their equivalent diameters using options -datacellcol and -datacellscale:
$ neper -V mytess.tess \
-datacellcol "real:file(mytess.stcell)" \
-datacellscale 0.15:0.20:0.25:0.30:0.35:0.40:0.45 \
-datacellscaletitle "Cell size (mm)" \
-print img5
This produces a PNG file named img5.png for the tessellation and a PNG file named img5-scale3.png for the scale bar.
To include the scale bar to the image, ImageMagick can be used:
$ convert img5.png img5-scale3.png -gravity East -composite img5.png
Speeding up Tessellation
When statistical properties (or other properties) are specified as input, Neper employs an interative approach, and so tessellation generation is longer than for a standard Voronoi tessellation. Even though the tessellation generation remains relatively fast, to speed up the tessellation process, a first way is through multithreading, as a performace increase is expected up about 16 threads. A second way is to modify the termination criterion, which is controlled by option -morphooptistop and set to val=1e-5 by default, which is relatively low. The value can be increased, or another criterion can be used.